In modern mathematics, a complex number is one of the most fundamental concepts, finding application both in “pure science” and in applied fields. It is clear that this was not always the case. In ancient times, when even ordinary negative numbers seemed a strange and dubious innovation, the need to extend the square root operation to them was not at all obvious. However, in the middle of the 16th century, mathematician Raphael Bombelli introduced complex (in this case, more precisely, imaginary) numbers into circulation. Actually, I propose to look at what was the essence of the difficulties that eventually brought the respectable Italian to such extremes.

There is a common misconception that complex numbers were required in order to solve quadratic equations. In fact, this is completely wrong: the task of finding the roots of a quadratic equation in no way motivates the introduction of complex numbers. That's perfect.

Let's see for ourselves. All sorts of things quadratic equation can be represented as:
.
Geometrically, this means that we want to find the intersection points of a certain line and a parabola
I even made a picture here for illustration.

As we all know well from school, the roots of a quadratic equation (in the above notations) are found by the following formula:

There are 3 possible options:
1. The radical expression is positive.
2. The radical expression is equal to zero.
3. The radical expression is negative.

In the first case there are 2 different roots, in the second there are two coinciding ones, in the third the equation “cannot be solved”. All these cases have a very clear geometric interpretation:
1. A straight line intersects a parabola (blue line in the figure).
2. A straight line touches a parabola.
3. The straight line has no common points with the parabola (lilac straight line in the figure).

The situation is simple, logical, and consistent. Try to extract square root There is absolutely no basis for a negative number. Nobody even tried.

The situation changed significantly when inquisitive mathematical thought reached cubic equations. A little less obvious, using some simple substitution , any cubic equation can be reduced to the form: . WITH geometric point From a visual perspective, the situation is similar to the previous one: we are looking for the intersection point of a straight line and a cubic parabola.
Take a look at the picture:

The significant difference from the case of a quadratic equation is that no matter what line we take, it will always intersect the parabola. That is, from purely geometric considerations, a cubic equation always has at least one solution.
You can find it using the Cardano formula:

Where
.
A little bulky, but so far everything seems to be in order. Or not?

In general, Cardano's formula is a vivid example of the “Arnold's principle” in action. And what is characteristic is that Cardano never claimed authorship of the formula.

Let us return, however, to our sheep. The formula is remarkable, without exaggeration, a great achievement of mathematics in the early to mid-16th century. But she has one nuance.
Let's take a classic example, which Bombelli considered:
.
Suddenly,
,
and, accordingly,
.
We've arrived. It’s a pity for the formula, but the formula is good. Dead end. Despite the fact that the equation certainly has a solution.

Rafael Bombelli's idea was as follows: let's pretend to be a hose and pretend that the root of a negative is some kind of number. We, of course, know that there are no such numbers, but nevertheless, let's imagine that it exists and, like ordinary numbers, it can be added to others, multiplied, raised to a power, etc.

Using a similar approach, Bombelli found, in particular, that
,
And
.
Let's check:
.
Please note that in the calculations no assumptions were made about the properties of the square roots of negative numbers, except for the assumption mentioned above that they behave like “ordinary” numbers.

In total we get . Which is quite the correct answer, which can be easily verified by direct substitution. It was a real breakthrough. Breakthrough into the complex plane.

However, such calculations look like some kind of magic, math trick. The attitude towards them as some kind of trick persisted among mathematicians for a very long time. Actually, the name “imaginary numbers”, invented by Rene Descartes for roots of negative numbers, fully reflects the attitude of mathematicians of those times towards such entertainment.

However, as time passed, the “trick” was used with constant success, the authority of “imaginary numbers” in the eyes of the mathematical community grew, restrained, however, by the inconvenience of their use. Only the receipt by Leonhard Euler (by the way, it was he who introduced the now commonly used designation for the imaginary unit) of the famous formula

opened the way for complex numbers to various areas of mathematics and its applications. But that's a completely different story.

Complex or imaginary numbers first appeared in Cardano's famous work "The Great Art, or on the Rules of Algebra" in 1545. In the opinion of the author, these numbers were not suitable for use. However, this claim was later refuted. In particular, Bombelli in 1572, when solving a cubic equation, substantiated the use of imaginary numbers. He compiled the basic rules for operations with complex numbers.

And yet for a long time in the mathematical world there was no single idea about the essence of complex numbers.

The symbol for imaginary numbers was first proposed by the outstanding mathematician Euler. The proposed symbolism looked like this: i = sqr -1, where i is imaginarius, which means fictitious. Euler's merit also includes the idea of ​​the algebraic closedness of the field of complex numbers.

So, the need for numbers of a new type arose when solving quadratic equations for the case D< 0 (где D - дискриминант квадратного уравнения). В настоящее время комплексные числа нашли широкое применение в физике и технике, гидро- и аэродинамике, теории упругости и т.п.

The graphical representation of complex numbers has the form: a + bi, where a and b are real numbers, and i is an imaginary unit, i.e. i 2 = -1. The number a is called the abscissa, and b is the ordinate of the complex number a + bi. Two complex numbers a + bi and a - bi are called conjugate complex numbers.

There are a number of rules associated with complex numbers:

• Firstly, real number and can be written in the form of a complex number: a+ 0 i or a - 0 i. For example, 5 + 0 i and 5 - 0 i mean the same number 5.
• Secondly, the complex number 0+ bi is called a purely imaginary number. The notation bi means the same as 0+ bi .
• Third, two complex numbers a + bi and c + di are considered equal if a = c and b = d. Otherwise, complex numbers are not equal.

Basic operations on complex numbers include:

In geometric representation, complex numbers, unlike real numbers, which are represented on the number line by dots, are marked by dots on coordinate plane. For this we take rectangular (Cartesian) coordinates with identical scales on the axes. In this case, the complex number a + bi will be represented by point P with abscissa a and ordinate b. This coordinate system is called complex plane.

Conjugate complex numbers have the same modulus.

• We will be based on connections, not on mechanical formulas.
• Let's consider complex numbers as a complement to our number system, the same as zero, fractional or negative numbers.
• We visualize ideas in graphics to better understand the essence, and not just present them in dry text.

And our secret weapon: learning by analogy. We'll get to complex numbers by starting with their ancestors, negative numbers. Here's a little guide for you:

For now, this table makes little sense, but let it be there. By the end of the article everything will fall into place.

Let's really understand what negative numbers are

Negative numbers are not so simple. Imagine that you are a European mathematician in the 18th century. You have 3 and 4, and you can write 4 – 3 = 1. It's simple.

But what is 3 – 4? What exactly does this mean? How can you take 4 cows away from 3? How can you have less than nothing?

Negative numbers were viewed as complete nonsense, something that “cast a shadow over the whole theory of equations” (Francis Maceres, 1759). Today it would be complete nonsense to think of negative numbers as something illogical and unhelpful. Ask your teacher if negative numbers violate basic math.

What happened? We invented a theoretical number that had useful properties. Negative numbers cannot be touched or felt, but they are good at describing certain relationships (like debt, for example). This is a very useful idea.

Instead of saying, “I owe you 30,” and reading the words to see if I'm in the black or in the black, I can just write down “-30” and know what that means. If I make money and pay off my debts (-30 + 100 = 70), I can easily write this transaction in a few characters. I'll be left with +70.

The plus and minus signs automatically capture the direction - you don't need a whole sentence to describe the changes after each transaction. Mathematics has become simpler, more elegant. It no longer matters whether negative numbers are "tangible" - they have beneficial properties, and we used them until they became firmly established in our everyday life. If someone you know has not yet understood the essence of negative numbers, now you will help them.

But let's not minimize human suffering: negative numbers were a real shift in consciousness. Even Euler, the genius who discovered the number e and much more, did not understand negative numbers as well as we do today. They were seen as "meaningless" results of calculations.

It is strange to expect children to calmly understand ideas that once confused even the best mathematicians.

Entering Imaginary Numbers

It's the same story with imaginary numbers. We can solve equations like this all day long:

The answers will be 3 and -3. But let’s imagine that some smart guy added a minus here:

Well, well. This is the kind of question that makes people cringe when they see it for the first time. Do you want to calculate the square root of a number less than zero? This is unthinkable! (Historically, similar questions actually existed, but it’s more convenient for me to imagine some faceless wise guy, so as not to embarrass the scientists of the past).

It looks crazy, just like negative numbers, zero and irrational numbers (non-repeating numbers) looked back in the day. There's no "real" meaning to this question, right?

No, it's not true. So-called “imaginary numbers” are as normal as any other (or just as abnormal): they are a tool for describing the world. In the same spirit that we imagine that -1, 0.3 and 0 "exist", let's suppose that there is some number i, where:

In other words, you multiply i by itself to get -1. What's happening now?

Well, at first we certainly have a headache. But by playing the game "Let's pretend that i exists" we actually make mathematics simpler and more elegant. New connections appear that we can easily describe.

You won't believe in i, just as those old grumpy mathematicians didn't believe in the existence of -1. All new concepts that twist the brain into a tube are difficult to perceive, and their meaning does not emerge immediately, even for the brilliant Euler. But as negative numbers have shown us, strange new ideas can be extremely useful.

I don't like the term "imaginary numbers" itself - it feels like it was chosen specifically to offend the feelings of i. The number i is as normal as the others, but the nickname “imaginary” has stuck to it, so we will also use it.

Visual understanding of negative and complex numbers

The equation x^2 = 9 actually means this:

Which transformation of x, applied twice, turns 1 into 9?

There are two answers: "x = 3" and "x = -3". That is, you can “scale by” 3 times or “scale by 3 and flip” (reversing or taking the reciprocal of the result are all interpretations of multiplying by negative one).

Now let's think about the equation x^2 = -1, which can be written like this:

Which transformation of x, applied twice, turns 1 into -1? Hm.

• We cannot multiply a positive number twice because the result will be positive.
• We can't multiply twice negative number, because the result will again be positive.

What about... rotation! It sounds unusual, of course, but what if we think of x as a “90 degree rotation”, then by applying x twice, we will make a 180 degree rotation on the coordinate axis, and 1 will turn into -1!

Wow! And if we think about it a little more, we can make two rotations in the opposite direction, and also go from 1 to -1. This is a "negative" rotation or multiplication by -i:

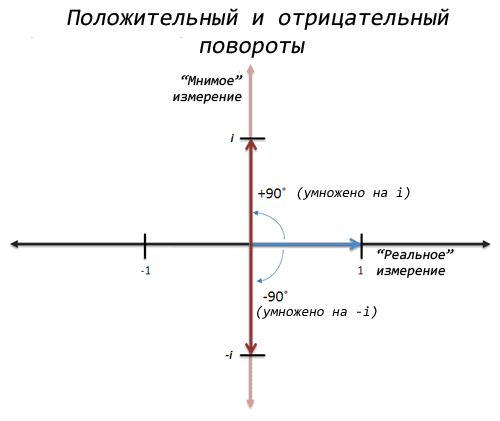
If we multiply by -i twice, then on the first multiplication we get -i from 1, and on the second -1 from -i. So there are actually two square roots of -1: i and -i.

This is pretty cool! We have something like a solution, but what does it mean?

• i is the "new imaginary dimension" for measuring number
• i (or -i) is what the numbers "become" when rotated
• Multiplying by i is rotating 90 degrees counterclockwise
• Multiplying by -i is a 90 degree clockwise rotation.
• Rotating twice in either direction gives -1: it takes us back to the "normal" dimension of positive and negative numbers (the x-axis).

All numbers are 2-dimensional. Yes, it's hard to accept, but it would have been just as hard for the ancient Romans to accept. decimals or long division. (How is it that there are more numbers between 1 and 2?). Looks weird like anyone new way think in mathematics.

We asked "How to turn 1 into -1 in two actions?" and found the answer: rotate 1 90 degrees twice. Quite a strange, new way of thinking in mathematics. But very useful. (By the way, this geometric interpretation of complex numbers appeared only decades after the discovery of the number i itself).

Also, do not forget that accepting a counterclockwise rotation as a positive result is a purely human convention, and everything could have been completely different.

Search for sets

Let's go a little deeper into the details. When you multiply negative numbers (like -1), you get a set:

• 1, -1, 1, -1, 1, -1, 1, -1

Since -1 does not change the size of the number, only the sign, you get the same number either with a “+” sign or with a “-” sign. For the number x you get:

• x, -x, x, -x, x, -x…

This is a very useful idea. The number "x" can represent good and bad weeks. Let's imagine that a good week follows a bad one; It's a good week; What will the 47th week be like?

X means it's going to be a bad week. See how negative numbers "follow the sign" - we can simply enter (-1)^47 into the calculator instead of counting ("Week 1 good, week 2 bad... week 3 good..."). Things that constantly alternate can be perfectly modeled using negative numbers.

Okay, what happens if we continue multiplying by i?

Very funny, let's simplify it all a little:

Here is the same thing presented graphically:

We repeat the cycle every 4th turn. That definitely makes sense, right? Any child will tell you that 4 turns to the left are the same as not turning at all. Now take a break from the imaginary numbers (i, i^2) and look at the total set:

• X, Y, -X, -Y, X, Y, -X, -Y…

Just as negative numbers model the mirror image of numbers, imaginary numbers can model anything that rotates between the two dimensions "X" and "Y". Or anything with a cyclical, circular dependence - do you have anything in mind?

Understanding Complex Numbers

There is one more detail to consider: can a number be both “real” and “imaginary”?

Don't even doubt it. Who said that we have to turn exactly 90 degrees? If we stand with one foot on the “real” dimension and the other on the “imaginary” one, it will look something like this:

We are at the 45 degree mark, where the real and imaginary parts are the same, and the number itself is “1 + i”. It's like a hot dog, where there is both ketchup and mustard - who said you have to choose one or the other?

Basically, we can choose any combination of real and imaginary parts and make a triangle out of it all. The angle becomes the "angle of rotation". A complex number is a fancy name for numbers that have a real and an imaginary part. They are written as “a + bi”, where:

• a - real part
• b - imaginary part

Not bad. But one final question remains: how “big” is a complex number? We cannot measure the real part or the imaginary part separately because we will miss the big picture.

Let's take a step back. The size of a negative number is the distance from zero:

This is another way to find absolute value. But how to measure both components at 90 degrees for complex numbers?

Is it a bird in the sky... or an airplane... Pythagoras is coming to the rescue!

This theorem pops up wherever possible, even in numbers invented 2000 years after the theorem itself. Yes, we are making a triangle, and its hypotenuse will be equal to the distance from zero:

Although measuring a complex number is not as simple as “just omitting the - sign,” complex numbers have very useful applications. Let's look at some of them.

Real Example: Rotations

We won't wait until college physics to practice complex numbers. We'll do this today. A lot can be said on the topic of multiplying complex numbers, but for now you need to understand the main thing:

• Multiplying by a complex number rotates by its angle

Let's see how it works. Imagine that I am on a boat, moving on a course of 3 units to the East every 4 units to the North. I want to change my course 45 degrees counterclockwise. What will my new course be?

Someone might say “It's easy! Calculate sine, cosine, google the tangent value... and then..." I think I broke my calculator...

Let's take a simpler route: we are on a course of 3 + 4i (it doesn't matter what the angle is, we don't care for now) and we want to turn 45 degrees. Well, 45 degrees is 1 + i (ideal diagonal). So we can multiply our rate by this number!

Here's the gist:

• Initial heading: 3 units East, 4 units North = 3 + 4i
• Rotate counterclockwise 45 degrees = multiply by 1 + i

When multiplied we get:

Our new guideline is 1 unit to the West (-1 to the East) and 7 units to the North, you can draw the coordinates on the graph and follow them.

But! We found the answer in 10 seconds, without any sines and cosines. There were no vectors, no matrices, no tracking of which quadrant we were in. It was simple arithmetic and a little algebra to work out the equation. Imaginary numbers are great for rotation!

Moreover, the result of such a calculation is very useful. We have course (-1, 7) instead of angle (atan(7/-1) = 98.13, and it is immediately clear that we are in the second quadrant. How, exactly, did you plan to draw and follow the indicated angle? Using a protractor at hand?

No, you would convert the angle to cosine and sine (-0.14 and 0.99), find the approximate ratio between them (about 1 to 7) and sketch a triangle. And here complex numbers undoubtedly win - accurately, lightning fast, and without a calculator!

If you're like me, you'll find this discovery mind-blowing. If not, I'm afraid that mathematics doesn't excite you at all. Sorry!

Trigonometry is good, but complex numbers make calculations much easier (like finding cos(a + b)). This is just a small announcement; in the following articles I will provide you with the complete menu.

Lyrical digression: some people think something like this: “Hey, it’s not convenient to have a North/East heading instead of a simple angle for the ship to follow!”

Is it true? Okay, look at yours right hand. What is the angle between the base of your little finger and the tip index finger? Good luck with your calculation method.

Or you can simply answer, “Well, the tip is X inches to the right and Y inches up,” and you can do something about it.

Are complex numbers getting closer?

We went through my basic discoveries in the field of complex numbers like a tornado. Look at the very first illustration, it should now become more clear.

There is so much more to discover in these beautiful, wonderful numbers, but my brain is already tired. My goal was simple:

• Convince you that complex numbers were only seen as “crazy”, but in fact they can be very useful (just like negative numbers)
• Show how complex numbers can simplify some problems like rotation.

If I seem overly concerned about this topic, there is a reason for that. Imaginary numbers have been an obsession of mine for years - the lack of understanding irritated me.

But lighting a candle is better than wading through pitch darkness: these are my thoughts, and I am sure that the light will light in the minds of my readers.

Epilogue: But they're still pretty weird!

I know they still look weird to me too. I'm trying to think like the first person who discovered zero thought.

Zero is such a strange idea, “something” represents “nothing”, and this could not be understood in any way in Ancient Rome. It's the same with complex numbers - it's a new way of thinking. But both zero and complex numbers greatly simplify mathematics. If we had never introduced weird things like new number systems, we would still be counting everything on our fingers.

I repeat this analogy because it is so easy to start thinking that complex numbers are "not normal." Let's be open to innovation: in the future, people will only joke about how someone until the 21st century did not believe in complex numbers.

When studying the properties of a quadratic equation, a restriction was set - for the discriminant less than zero there is no solution. It was immediately stated that we were talking about a set of real numbers. The inquisitive mind of a mathematician will be interested in what secret is contained in the clause about real values?

Over time, mathematicians introduced the concept of complex numbers, where the conditional value of the second root of minus one is taken as one.

Historical background

Mathematical theory develops sequentially, from simple to complex. Let's figure out how the concept called “complex number” arose and why it is needed.

Since time immemorial, the basis of mathematics has been ordinary counting. The researchers knew only the natural set of values. Addition and subtraction were simple. As economic relations became more complex, multiplication began to be used instead of adding identical values. Appeared reverse operation to multiplication - division.

The concept of a natural number limited the use of arithmetic operations. It is impossible to solve all division problems on a set of integer values. led first to the concept of rational meanings, and then to irrational meanings. If for rational it is possible to indicate the exact location of a point on a line, then for irrational it is impossible to indicate such a point. You can only approximately indicate the location interval. The combination of rational and irrational numbers formed a real set, which can be represented as a certain line with a given scale. Each step along the line is a natural number, and between them are rational and irrational values.

The era of theoretical mathematics began. The development of astronomy, mechanics, and physics required the solution of increasingly complex equations. In general form, the roots of the quadratic equation were found. When solving a more complex cubic polynomial, scientists encountered a contradiction. The concept of a negative cube root makes sense, but for a square root it results in uncertainty. In this case, the quadratic equation is only special case cubic.

In 1545, the Italian G. Cardano proposed introducing the concept of an imaginary number.

This number became the second root of minus one. The term complex number was finally formed only three hundred years later, in the works of the famous mathematician Gauss. He proposed to formally extend all the laws of algebra to an imaginary number. The real line has expanded to a plane. The world has become bigger.

Basic Concepts

Let us recall a number of functions that have restrictions on the real set:

• y = arcsin(x), defined in the range of values ​​between negative and positive unity.
• y = ln(x), makes sense for positive arguments.
• square root y = √x, calculated only for x ≥ 0.

By denoting i = √(-1), we introduce such a concept as an imaginary number, this will allow us to remove all restrictions from the domain of definition of the above functions. Expressions like y = arcsin(2), y = ln(-4), y = √(-5) take on meaning in a certain space of complex numbers.

The algebraic form can be written as z = x + i×y on the set of real values ​​x and y, and i 2 = -1.

The new concept removes all restrictions on the use of any algebraic function and its appearance resembles a graph of a straight line in the coordinates of real and imaginary values.

Complex plane

The geometric form of complex numbers makes it possible to visualize many of their properties. Along the Re(z) axis we mark the real values ​​of x, along the Im(z) - imaginary values ​​of y, then the point z on the plane will display the required complex value.

Definitions:

• Re(z) - real axis.
• Im(z) - means the imaginary axis.
• z is the conditional point of a complex number.
• Numerical value the length of the vector from the zero point to z is called the modulus.
• The real and imaginary axes divide the plane into quarters. With a positive coordinate value - I quarter. When the argument of the real axis is less than 0, and the imaginary axis is greater than 0 - the second quarter. When the coordinates are negative - III quarter. The last, IV quarter contains many positive real values ​​and negative imaginary values.

Thus, on a plane with coordinate values ​​x and y, you can always visually depict a point of a complex number. The symbol i is introduced to separate the real part from the imaginary part.

Properties

1. With a zero value of the imaginary argument, we simply obtain a number (z = x), which is located on the real axis and belongs to the real set.
2. Special case, when the value of the real argument becomes zero, the expression z = i×y corresponds to the location of the point on the imaginary axis.
3. The general form z = x + i×y will be for non-zero values ​​of the arguments. Indicates the location of the point characterizing a complex number in one of the quarters.

Trigonometric notation

Let's remember the polar coordinate system and the definition of sin and cos. Obviously, using these functions you can describe the location of any point on the plane. To do this, it is enough to know the length of the polar ray and the angle of inclination to the real axis.

Definition. A notation of the form ∣z ∣ multiplied by the sum of the trigonometric functions cos(ϴ) and the imaginary part i ×sin(ϴ) is called a trigonometric complex number. Here we use the notation angle of inclination to the real axis

ϴ = arg(z), and r = ∣z∣, the beam length.

From the definition and properties of trigonometric functions, a very important Moivre formula follows:

z n = r n × (cos(n × ϴ) + i × sin(n × ϴ)).

Using this formula, it is convenient to solve many systems of equations containing trigonometric functions. Especially when the problem of exponentiation arises.

Module and phase

To complete the description of a complex set, we propose two important definitions.

Knowing the Pythagorean theorem, it is easy to calculate the length of the ray in the polar coordinate system.

r = ∣z∣ = √(x 2 + y 2), such a notation in complex space is called “modulus” and characterizes the distance from 0 to a point on the plane.

The angle of inclination of the complex ray to the real line ϴ is usually called the phase.

From the definition it is clear that the real and imaginary parts are described using cyclic functions. Namely:

• x = r × cos(ϴ);
• y = r × sin(ϴ);

Conversely, the phase has a connection with algebraic values through the formula:

ϴ = arctan(x / y) + µ, the correction µ is introduced to take into account the periodicity of geometric functions.

Euler's formula

Mathematicians often use the exponential form. The numbers of the complex plane are written as the expression

z = r × e i × ϴ, which follows from Euler’s formula.

This notation has become widespread for practical calculations. physical quantities. The form of representation in the form of exponential complex numbers is especially convenient for engineering calculations, where there is a need to calculate circuits with sinusoidal currents and it is necessary to know the value of the integrals of functions with a given period. The calculations themselves serve as a tool in the design of various machines and mechanisms.

Defining Operations

As already noted, all algebraic laws of working with basic mathematical functions apply to complex numbers.

Sum operation

When adding complex values, their real and imaginary parts also add up.

z = z 1 + z 2, where z 1 and z 2 are complex numbers general view. Transforming the expression, after opening the brackets and simplifying the notation, we get the real argument x = (x 1 + x 2), imaginary argument y = (y 1 + y 2).

On the graph it looks like the addition of two vectors, according to the well-known parallelogram rule.

Subtraction operation

It is considered as a special case of addition, when one number is positive, the other is negative, that is, located in the mirror quarter. The algebraic notation looks like the difference between the real and imaginary parts.

z = z 1 - z 2 , or, taking into account the values ​​of the arguments, similar to the addition operation, we obtain for real values ​​x = (x 1 - x 2) and imaginary values ​​y = (y 1 - y 2).

Multiplication in the complex plane

Using the rules for working with polynomials, we will derive a formula for solving complex numbers.

Following the general algebraic rules z=z 1 ×z 2, we describe each argument and present similar ones. The real and imaginary parts can be written as follows:

• x = x 1 × x 2 - y 1 × y 2,
• y = x 1 × y 2 + x 2 × y 1.

It looks more beautiful if we use exponential complex numbers.

The expression looks like this: z = z 1 × z 2 = r 1 × e i ϴ 1 × r 2 × e i ϴ 2 = r 1 × r 2 × e i(ϴ 1+ ϴ 2) .

Division

When considering the division operation as the inverse of the multiplication operation, in exponential notation we obtain a simple expression. Dividing the value of z 1 by z 2 is the result of dividing their modules and the phase difference. Formally, when using the exponential form of complex numbers, it looks like this:

z = z 1 / z 2 = r 1 × e i ϴ 1 / r 2 × e i ϴ 2 = r 1 / r 2 × e i(ϴ 1- ϴ 2) .

In the form of algebraic notation, the operation of dividing numbers in the complex plane is written a little more complicated:

By describing the arguments and carrying out transformations of polynomials, it is easy to obtain the values ​​x = x 1 × x 2 + y 1 × y 2 , respectively y = x 2 × y 1 - x 1 × y 2 , however, within the framework of the described space this expression makes sense, if z 2 ≠ 0.

Extracting the root

All of the above can be used to define more complex algebraic functions - raising to any power and its inverse - extracting the root.

Taking advantage general concept raising to the power n, we get the definition:

z n = (r × e i ϴ) n .

Using general properties, we rewrite it in the form:

z n = r n × e i ϴ n .

Received simple formula raising a complex number to a power.

From the definition of degree we obtain a very important corollary. An even power of the imaginary unit is always equal to 1. Any odd power of the imaginary unit is always equal to -1.

Now let's study inverse function- root extraction.

For simplicity of notation, we take n = 2. The square root w of a complex value z on the complex plane C is usually considered to be the expression z = ±, valid for any real argument greater than or equal to zero. For w ≤ 0 there is no solution.

Let's look at the simplest quadratic equation z 2 = 1. Using the formulas for complex numbers, we rewrite r 2 × e i 2ϴ = r 2 × e i 2ϴ = e i 0. From the record it is clear that r 2 = 1 and ϴ = 0, therefore, we have the only solution, equal to 1. But this contradicts the concept that z = -1, also consistent with the definition of a square root.

Let's figure out what we don't take into account. If we remember the trigonometric notation, we will restore the statement - with a periodic change in the phase ϴ, the complex number does not change. Let us denote the value of the period by the symbol p, then the following is valid: r 2 × e i 2ϴ = e i (0+ p), from which 2ϴ = 0 + p, or ϴ = p / 2. Therefore, e i 0 = 1 and e i p /2 = -1 . We obtained the second solution, which corresponds to the general understanding of the square root.

So, to find an arbitrary root of a complex number, we will follow the procedure.

• Let's write the exponential form w= ∣w∣ × e i (arg (w) + pk), k is an arbitrary integer.
• We can also represent the required number using the Euler form z = r × e i ϴ .
• Let's take advantage general definition root extraction functions r n *e i n ϴ = ∣w∣ × e i (arg (w) + pk) .
• From the general properties of equality of modules and arguments, we write r n = ∣w∣ and nϴ = arg (w) + p×k.
• The final notation for the root of a complex number is described by the formula z = √∣w∣ × e i (arg (w) + pk) / n.
• Comment. The value ∣w∣, by definition, is a positive real number, which means that the root of any power makes sense.

Field and mate

In conclusion, we give two important definitions that are of little importance for solving applied problems with complex numbers, but are essential for further development mathematical theory.

Expressions for addition and multiplication are said to form a field if they satisfy the axioms for any elements of the complex plane z:

1. Changing the places of complex terms does not change the complex sum.
2. The statement is true - in complex expression any sum of two numbers can be replaced by their value.
3. There is a neutral value 0 for which z + 0 = 0 + z = z is true.
4. For any z there is an opposite - z, the addition of which gives zero.
5. When changing the places of complex factors, the complex product does not change.
6. The multiplication of any two numbers can be replaced by their value.
7. There is a neutral value 1, multiplying by which does not change the complex number.
8. For every z ≠ 0, there is an inverse value z -1, multiplying by which results in 1.
9. Multiplying the sum of two numbers by a third is equivalent to the operation of multiplying each of them by this number and adding the results.
10. 0 ≠ 1.

The numbers z 1 = x + i×y and z 2 = x - i×y are called conjugate.

Theorem. For pairing, the following statement is true:

• The conjugate of a sum is equal to the sum of the conjugate elements.
• The conjugate of a product is equal to the product of conjugates.
• equal to the number itself.

In general algebra, such properties are usually called field automorphisms.

Examples

Following the given rules and formulas for complex numbers, you can easily operate with them.

Let's look at the simplest examples.

Task 1. Using the equation 3y +5 x i= 15 - 7i, determine x and y.

Solution. Let us recall the definition of complex equalities, then 3y = 15, 5x = -7. Therefore x = -7 / 5, y = 5.

Task 2. Calculate the values ​​of 2 + i 28 and 1 + i 135.

Solution. Obviously, 28 is an even number, from the corollary of the definition of a complex number to the power we have i 28 = 1, which means the expression is 2 + i 28 = 3. The second value, i 135 = -1, then 1 + i 135 = 0.

Task 3. Calculate the product of the values ​​2 + 5i and 4 + 3i.

Solution. From the general properties of multiplication of complex numbers we obtain (2 + 5i)X(4 + 3i) = 8 - 15 + i(6 + 20). The new value will be -7 + 26i.

Task 4. Calculate the roots of the equation z 3 = -i.

Solution. There may be several options for finding a complex number. Let's consider one of the possible ones. By definition, ∣ - i∣ = 1, the phase for -i is -p / 4. The original equation can be rewritten as r 3 *e i 3ϴ = e - p/4+ pk, from where z = e - p / 12 + pk /3 , for any integer k.

The set of solutions has the form (e - ip/12, e ip /4, e i 2 p/3).

Why are complex numbers needed?

History knows many examples when scientists, working on a theory, do not even think about the practical application of their results. Mathematics is, first of all, a game of the mind, a strict adherence to cause-and-effect relationships. Almost everything mathematical constructions are reduced to solving integral and differential equations, and those, in turn, with some approximation, are solved by finding the roots of the polynomials. Here we first encounter the paradox of imaginary numbers.

Scientific natural scientists, solving completely practical problems, resorting to solutions of various equations, discover mathematical paradoxes. The interpretation of these paradoxes leads to completely surprising discoveries. Dual nature electromagnetic waves one such example. Complex numbers play a decisive role in understanding their properties.

This, in turn, found practical application in optics, radio electronics, energy and many other technological fields. Another example, much harder to understand physical phenomena. Antimatter was predicted at the tip of the pen. And only many years later attempts to physically synthesize it begin.

One should not think that such situations exist only in physics. No less interesting discoveries occur in living nature, during the synthesis of macromolecules, during the study of artificial intelligence. And all this thanks to the expansion of our consciousness, moving away from simple addition and subtraction of natural quantities.

Complex numbers for dummies. Lesson 1. What are they and what are they eaten with. Imaginary unit.

In order to understand what complex numbers are, let's remember about ordinary numbers and take a comprehensive look at them. And so, the simplest thing is natural numbers. They are called natural because through them something can be expressed “in kind,” that is, something can be counted. Here are two apples. They can be counted. There are five boxes of chocolates. We can count them. In other words, natural numbers- these are numbers with which we can count specific objects. You know very well that these numbers can be added, subtracted, multiplied and divided. Everything is clear with addition and multiplication. There were two apples, they added three, it became five. We took three boxes of chocolates, 10 pieces each, which means a total of thirty chocolates. Now let's move on to whole numbers. If natural numbers denote a specific number of objects, then abstractions are introduced into the set of integers. This zero And negative numbers. Why are these abstractions? Zero is the absence of something. But can we touch, feel what is not there? We can touch two apples, here they are. We can even eat them. What does zero apples mean? Can we touch, feel this zero? No, we can't. So this is abstraction. You have to somehow indicate the absence of something. So we designated zero as a number. But why signify this somehow? Let's imagine that we had two apples. We ate two. How much do we have left? That's right, not at all. We will write this operation (we ate two apples) as subtraction 2-2. And what did we end up with? How should we label the result? Only by introducing a new abstraction (zero), which will indicate that as a result of subtraction (eating) it turns out that we do not have a single apple left. But we can subtract not 2, but 3 from two. It would seem that this operation is meaningless. If we only have two apples, how can we eat three?

Let's look at another example. We go to the store for beer. We have 100 rubles with us. Beer costs 60 rubles per bottle. We want to buy two bottles, but we don’t have enough money. We need 120 rubles. And then we meet our old friend and borrow twenty from him. We buy beer. Question. How much money do we have left? Common sense dictates that not at all. But from a mathematical point of view this would be absurd. Why? Because in order to get zero as a result, you need to subtract 100 from 100. And we do 100-120. Here we should get something else. What did we get? And the fact that we still owe our friend 20 rubles. The next time we have 140 rubles with us, we will come to the store for beer, meet a friend, pay off our debts with him and be able to buy two more bottles of beer. As a result, we get 140-120-20=0. Note the -20. This is another abstraction - negative number. That is, our debt to a friend is a number with a minus sign, because when we repay the debt, we subtract this amount. I will say more, this is an even greater abstraction than zero. Zero means something that doesn't exist. And a negative number is like something that will be taken away from us in the future.

And so, using an example, I showed how abstractions are born in mathematics. And that, it would seem, despite all the absurdity of such abstractions (like taking away more than was), they find application in real life. In the case of dividing integers, another abstraction arises - fractional numbers. I will not dwell on them in detail, and it is clear that they are needed in the case when we have integers that are not divisible by an integer. For example, we have four apples, but we need to divide them among three people. It’s clear here that we divide the one remaining apple into three parts and get fractions.

Now let’s very smoothly get to the complex numbers themselves. But first, remember that when you multiply two negative numbers, you get a positive number. Someone ask - why is this so? Let's first understand multiplying a negative number by a positive one. Let's say we multiply -20 by 2. That is, we need to add -20+-20. The result is -40, since adding a negative number is a subtraction. Why subtraction - see above, a negative number is a debt; when we take it away, something is taken away from us. There is another everyday meaning. What happens if the debt increases? For example, in the case when we were given a loan at interest? As a result, the same number with a minus sign remained, the one that became larger after the minus. What does it mean to multiply by a negative number? What does 3*-2 mean? This means that the number three must be taken minus two times. That is, put a minus before the result of multiplication. By the way, this is the same as -3*2, since rearranging the factors does not change the product. Now pay attention. Multiply -3 by -2. We take the number -3 minus two times. If we take the number -3 twice, then the result will be -6, you understand that. What if we take minus two times? But what does it mean to take minus times? If you take a positive number minus times, you end up with a negative number, its sign changes. If we take a negative number minus times, then its sign changes and it becomes positive.

Why did we talk about multiplying minus by minus? And in order to consider another abstraction, this time it is directly related to complex numbers. This imaginary unit. The imaginary unit is equal to the square root of minus 1:

Let me remind you what a square root is. This is the inverse operation of squaring. And squaring is multiplying a number by itself. So the square root of 4 is 2 because 2*2=4. The square root of 9 is 3, since 3*3=9. The square root of one also turns out to be one, and the square root of zero is zero. But how do we take the square root of minus one? What number must be multiplied by itself to get -1? But there is no such number! If we multiply -1 by itself, we will end up with 1. If we multiply 1 by 1, we will get 1. And we won’t get minus -1 in this way. But, nevertheless, we may encounter a situation where there is a negative number under the root. What to do? You can, of course, say that there is no solution. It's like dividing by zero. Until some time, we all believed that it was impossible to divide by zero. But then we learned about such an abstraction as infinity, and it turned out that dividing by zero is still possible. Moreover, abstractions such as division by zero, or the uncertainty obtained by dividing zero by zero or infinity by infinity, as well as other similar operations, are widely used in higher mathematics (), and higher mathematics is the basis of many exact sciences, which move forward technical progress. So maybe in the imaginary unit there is some kind of secret meaning? Eat. And you will understand it by reading my further lessons on complex numbers. In the meantime, I will talk about some areas where complex numbers (numbers that contain an imaginary unit) are used.

And so, here is a list of areas where complex numbers are used:

Electrical engineering. Calculation of alternating current circuits. The use of complex numbers in this case greatly simplifies the calculation; without them, differential and integral equations would have to be used.

Quantum mechanics.In short - in quantum mechanics there is such a thing as wave function, which itself is complex-valued and whose square (already a real number) is equal to the probability density of finding a particle at a given point. See also the series of lessons

Digital signal processing. Theory digital processing signals includes such a concept as the z-transform, which greatly facilitates various calculations related to the calculation of the characteristics of various signals, such as frequency and amplitude characteristics, etc.

Description of processes of plane flow of liquids.

Liquid flow around profiles.

Wave movements of liquid.

And this is far from an exhaustive list of where complex numbers are used. This completes the first acquaintance with complex numbers, until we meet again.